Debian-projectleiderverkiezing 2025
Tijdslijn
| Nominatieperiode: | Zondag 09-03-2025 00:00:00 UTC | Zaterdag 15-03-2025 23:59:59 UTC |
|---|---|---|
| Campagneperiode: | Zondag 16-03-2025 00:00:00 UTC | Zaterdag 05-04-2025 23:59:59 UTC |
| Stemperiode: | Zondag 06-04-2025 00:00:00 UTC | Zaterdag 19-04-2025 23:59:59 UTC |
Houd er rekening mee dat de nieuwe termijn van de projectleider ingaat op 21-04-2025.
Nominaties
- Gianfranco Costamagna [locutusofborg@debian.org] [nominatie-e-mail] [programmaverklaring]
- Julian Andres Klode [jak@debian.org] [nominatie-e-mail] [programmaverklaring]
- Andreas Tille [tille@debian.org] [nominatie-e-mail] [programmaverklaring]
- Sruthi Chandran [srud@debian.org] [nominatie-e-mail] [programmaverklaring]
Als het stembiljet klaar is, kan het per e-mail worden aangevraagd door een ondertekende e-mail te sturen naar ballot@vote.debian.org met als onderwerp leader2025.
Data en Statistieken
Zoals steeds worden ook dit jaar statistieken verzameld over ontvangen stembiljetten en verzonden ontvangstbevestigingen tijdens de stemperiode. Bovendien wordt de lijst van kiezers geregistreerd. Ook zal de scoretabel ter inzage worden gelegd. Houd er rekening mee dat de projectleider bij geheime stemming verkozen wordt, dus zal de scoretabel niet de namen van de kiezers bevatten, maar een HMAC waarmee de kiezers kunnen controleren of hun stem op de lijst met uitgebrachte stemmen staat. Voor elke kiezer wordt een sleutel gegenereerd die samen met de ontvangstbevestiging van de uitgebrachte stem wordt meegestuurd.
Quorum
Met de huidige lijst met stemgerechtigde ontwikkelaars, hebben we:
Huidig aantal ontwikkelaars = 1030
Q ( sqrt(#ontwikkelaars) / 2 ) = 16.0468065358812
K min(5, Q ) = 5
Quorum (3 x Q ) = 48.1404196076436
Quorum
- Optie 1 behaalde het quorum: 273 > 48.1404196076436
- Optie 2 behaalde het quorum: 264 > 48.1404196076436
- Optie 3 behaalde het quorum: 318 > 48.1404196076436
- Optie 4 behaalde het quorum: 225 > 48.1404196076436
Meerderheidsvereiste
De kandidaten hebben een gewone meerderheid nodig om in aanmerking te komen.
Meerderheid
- Optie 1 slaagt voor de meerderheid. 3.900 (273/70) > 1
- Optie 2 slaagt voor de meerderheid. 3.259 (264/81) > 1
- Optie 3 slaagt voor de meerderheid. 8.154 (318/39) > 1
- Optie 4 slaagt voor de meerderheid. 2.009 (225/112) > 1
Uitslag
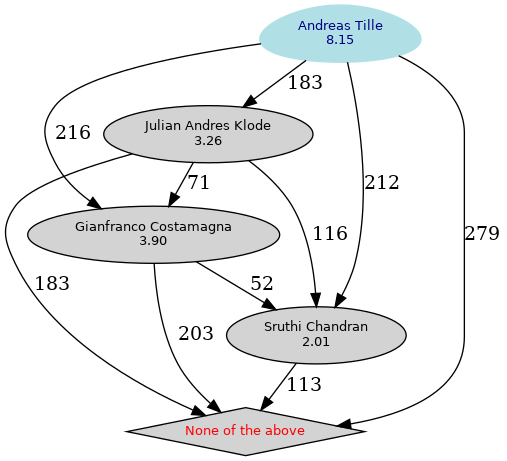
In de bovenstaande grafiek duiden alle roze gekleurde knooppunten erop dat de optie de meerderheid niet heeft gehaald, het blauwe geeft de winnaar aan. Een achthoek wordt gebruikt voor de opties die niet boven de standaard uitkwamen.
- Option 1 "Gianfranco Costamagna"
- Option 2 "Julian Andres Klode"
- Option 3 "Andreas Tille"
- Option 4 "Sruthi Chandran"
- Option 5 "Geen van bovenstaande"
In de volgende tabel geeft het vak[rij x][kol y] weer hoeveel keer optie x verkozen werd boven optie y tijdens de stemming. Een meer gedetailleerde uitleg over de vergelijkingsmatrix kan helpen om de tabel te begrijpen. Om inzicht te krijgen in de Condorcet-methode, is het Wikipedia-artikel redelijk leerzaam.
| Optie | |||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| Optie 1 | 110 | 66 | 179 | 273 | |
| Optie 2 | 181 | 78 | 211 | 264 | |
| Optie 3 | 282 | 261 | 278 | 318 | |
| Optie 4 | 127 | 95 | 66 | 225 | |
| Optie 5 | 70 | 81 | 39 | 112 | |
Bekijken we rij 2, kolom 1, dan blijkt dat Julian Andres Klode
181 keer verkozen werd boven Gianfranco Costamagna
Bekijken we rij 1, kolom 2, dan blijkt dat Gianfranco Costamagna
110 keer verkozen werd boven Julian Andres Klode.
Paarsgewijze vergelijking
- Optie 2 verslaat optie 1 met ( 181 - 110) = 71 stemmen.
- Optie 3 verslaat optie 1 met ( 282 - 66) = 216 stemmen.
- Optie 1 verslaat optie 4 met ( 179 - 127) = 52 stemmen.
- Optie 1 verslaat optie 5 met ( 273 - 70) = 203 stemmen.
- Optie 3 verslaat optie 2 met ( 261 - 78) = 183 stemmen.
- Optie 2 verslaat optie 4 met ( 211 - 95) = 116 stemmen.
- Optie 2 verslaat optie 5 met ( 264 - 81) = 183 stemmen.
- Optie 3 verslaat optie 4 met ( 278 - 66) = 212 stemmen.
- Optie 3 verslaat optie 5 met ( 318 - 39) = 279 stemmen.
- Optie 4 verslaat optie 5 met ( 225 - 112) = 113 stemmen.
De Schwartz-verzameling bevat
- Optie 3 "Andreas Tille"
De winnaars
- Optie 3 "Andreas Tille"
Debian gebruikt de Condorcet-methode bij stemmingen.
Simpel gesteld kan de gewone Condorcet-methode als volgt
worden uitgedrukt:
Bekijk alle mogelijke wedlopen in twee richtingen
tussen kandidaten. De Condorcet-winnaar, als er een is,
is de kandidaat die elke andere kandidaat kan verslaan
in een wedloop met die kandidaat in de twee richtingen.
Het probleem is dat er bij complexe verkiezingen wel eens
sprake kan zijn van een circulaire relatie waarin A
B verslaat, B C verslaat en C A verslaat. De meeste
variaties op Condorcet gebruiken verschillende manieren om
deze onbesliste stand op te lossen. Zie
de methode van het kloonbestendig sequentieel uitrangeren in een Schwartz-verzameling
voor details. De variatie die Debian gebruikt wordt
beschreven in de
statuten,
meer bepaald in sectie A.5.
Debian-projectsecretaris